nesman
It's all about learningMay 13, 2008 Archives
Tue May 13 15:18:39 CDT 2008
Tried to Count in Base3 got 3-Sided Fractal
Recently, I got a wild hair in an uncomfortable place that suggested I look into trinary counting.
Binary is great, but it doesn't seen very efficient.
Each number holder is seen as either 0% or 100%.
It would be nice to use a more precise system.
Instead of splitting each digit in half, give 3 possibilities.
To test this, I tried to visualize how I might build a counting machine that worked in binary, but represented a base 3 system. I'm pretty sure that I got it wrong. My plan was to have a line of toggle switches that would flip (or not) based on the value of the previous switch. Each increment would toggle the switch on the right, so the next switch would only be flipped every other time. I wasn't sure, but I figured this might be a good place to start. My experiment in testing this had interesting results.
After working on it for a while, I began to picture it as a bucket brigade. The digit on the far right (Number 0) was the bucket brigadier in charge of the spigot. (We call him Number 0 because he doesn't know how to catch. This is why he's in charge of the spigot.) Each second, Number 0 fills his bucket and throws it to the next person (Number 1). If the next person has an empty bucket, he catches the water and turns to face the next person in line. The next second, everybody with water in their bucket throws some to the next person. They only throw half of the water, to make sure they never run out. (Don't worry about this part too much. Just run with it) They continue doing this until they are hit in the back of the head with water from the previous person, which causes them to turn around and prepare to catch the next bucket.
In this system, Number 0 will flip Number 1 each second. Number 2 (the next person) will catch a bucket of water (either in her own bucket or to the back of her head) every other second. This will cause Number 3 to flip every 3 seconds and so forth. In this way, the first bucket of water takes 1 second per person to make it to the end of the line. Following buckets are more and more likely to end up being wasted, but it makes for an interesting counting experiment.
To help me visualize this, I would need a script to calculate the state of each person in line, each second. The main mechanic is that each digit is flipped only if the previous is in the "on" position (throwing water). Eventually I figured that I could represent each state as 1 or -1. To determine what happens to any particular digit, just multiply it by the one on it's right. Here, we consider 1 to be "off" because multiplying causes no change, while -1 is "on" because it will toggle negative status. Unfortunately, 1 and -1 are not very pretty in large groups; they just look like vertical and horizontal dashes.
Before I could go much further, I had to figure out how to do my calculations with 1 and -1 while displaying something that looked decent. I ended up with two arrays: all of my heavy lifting was done in the first, then the pattern was copied to the second as a prettier version. My first thought was to use an if/then selection to swap the value: if $val == -1 { then $binval = 0 }; That just felt lazy. I never tested it, but I'm sure that's two slow. Finally I found a method to convert either value to 1 or 0 from 1 or -1: $binvar = (($var +1) / 2); This will use -1 to toggle, but display 0 for better contrast.
Finally, it's time to run it and watch my numbers run. An early test looked like this: (each second is displayed below the previous, and counting starts from the right)
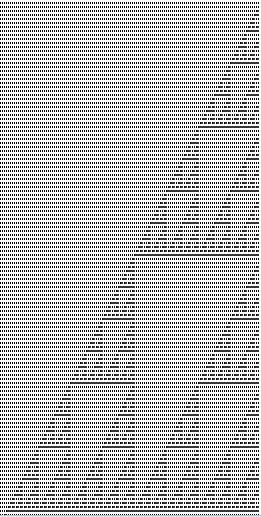
My result was a kind of tilted Sierpinski Triangle. Although I completely failed to count in base 3, I succeeded in building a 3-sided fractal.
The final version of my code can be found here: negcount.php You should be able to run this on any web server with php4 if you would like to play with it.
Update:After a little research, I see others with code for the same thing. Jason Underdown wrote Sierpinski's Triangle in C which is 3 times as long as mine, if you count comments and twice as long without comments. (Found via Wikipedia article for Sierpinski Triangle).
Before I brag too much, I should point out this example (done in Ruby) of a one-liner Sierpinski's Triangle:
To test this, I tried to visualize how I might build a counting machine that worked in binary, but represented a base 3 system. I'm pretty sure that I got it wrong. My plan was to have a line of toggle switches that would flip (or not) based on the value of the previous switch. Each increment would toggle the switch on the right, so the next switch would only be flipped every other time. I wasn't sure, but I figured this might be a good place to start. My experiment in testing this had interesting results.
After working on it for a while, I began to picture it as a bucket brigade. The digit on the far right (Number 0) was the bucket brigadier in charge of the spigot. (We call him Number 0 because he doesn't know how to catch. This is why he's in charge of the spigot.) Each second, Number 0 fills his bucket and throws it to the next person (Number 1). If the next person has an empty bucket, he catches the water and turns to face the next person in line. The next second, everybody with water in their bucket throws some to the next person. They only throw half of the water, to make sure they never run out. (Don't worry about this part too much. Just run with it) They continue doing this until they are hit in the back of the head with water from the previous person, which causes them to turn around and prepare to catch the next bucket.
In this system, Number 0 will flip Number 1 each second. Number 2 (the next person) will catch a bucket of water (either in her own bucket or to the back of her head) every other second. This will cause Number 3 to flip every 3 seconds and so forth. In this way, the first bucket of water takes 1 second per person to make it to the end of the line. Following buckets are more and more likely to end up being wasted, but it makes for an interesting counting experiment.
To help me visualize this, I would need a script to calculate the state of each person in line, each second. The main mechanic is that each digit is flipped only if the previous is in the "on" position (throwing water). Eventually I figured that I could represent each state as 1 or -1. To determine what happens to any particular digit, just multiply it by the one on it's right. Here, we consider 1 to be "off" because multiplying causes no change, while -1 is "on" because it will toggle negative status. Unfortunately, 1 and -1 are not very pretty in large groups; they just look like vertical and horizontal dashes.
Before I could go much further, I had to figure out how to do my calculations with 1 and -1 while displaying something that looked decent. I ended up with two arrays: all of my heavy lifting was done in the first, then the pattern was copied to the second as a prettier version. My first thought was to use an if/then selection to swap the value: if $val == -1 { then $binval = 0 }; That just felt lazy. I never tested it, but I'm sure that's two slow. Finally I found a method to convert either value to 1 or 0 from 1 or -1: $binvar = (($var +1) / 2); This will use -1 to toggle, but display 0 for better contrast.
Finally, it's time to run it and watch my numbers run. An early test looked like this: (each second is displayed below the previous, and counting starts from the right)
1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 0 0 1 1 1 0 1 1 1 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1Remember that here, 1 is off, 0 is on for the ability to toggle the number next to you. Also, the number on the right is toggled for each new row. This is OK to do manually for small numbers, but to really test the concept, I wanted to run it with hundreds of columns and rows at once. Since 1's and 0's take up more room than needed, I loaded the result into opera and zoomed out. Here is a screen shot of my result:
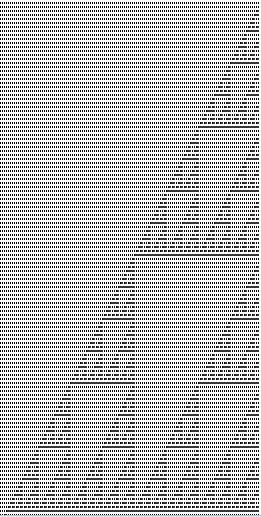
My result was a kind of tilted Sierpinski Triangle. Although I completely failed to count in base 3, I succeeded in building a 3-sided fractal.
The final version of my code can be found here: negcount.php You should be able to run this on any web server with php4 if you would like to play with it.
Update:After a little research, I see others with code for the same thing. Jason Underdown wrote Sierpinski's Triangle in C which is 3 times as long as mine, if you count comments and twice as long without comments. (Found via Wikipedia article for Sierpinski Triangle).
Before I brag too much, I should point out this example (done in Ruby) of a one-liner Sierpinski's Triangle:
ruby -le '64.times{|y|print" "*(63-y),(0..y).map{|x|~y&x>0?" .":" A"}}'